Intro to Stats
Introduction to Basic Stats in R
Code from session
#Independent-Samples T-test
#Create variables
Women = c(99, 85, 78, 93, 95, 87)
Men = c(72, 75, 70, 68, 70, 80)
#T-test to see if men and women's scores significantly differ
t.test(Women,Men,alternative="two.sided")
##
## Welch Two Sample t-test
##
## data: Women and Men
## t = 4.7332, df = 7.9586, p-value = 0.001498
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 8.71012 25.28988
## sample estimates:
## mean of x mean of y
## 89.5 72.5
#One-sample t-test to see if women scored significantly lower than 95% on the test
t.test(Women, alternative = "less", mu = 95)
##
## One Sample t-test
##
## data: Women
## t = -1.7644, df = 5, p-value = 0.06897
## alternative hypothesis: true mean is less than 95
## 95 percent confidence interval:
## -Inf 95.78122
## sample estimates:
## mean of x
## 89.5
#One-way analysis of variance
#Read sample pain score data into R
pain = c(4, 5, 4, 3, 2, 4, 3, 4, 4, 6, 8, 4, 5, 4, 6, 5, 8, 6, 6, 7, 6, 6, 7, 5, 6, 5, 5)
gender = c("F", "F", "F", "M", "M", "M", "M", "F", "F", "M", "M", "F", "F", "F", "M", "F", "M", "M", "M", "F", "F", "F", "F", "M", "F", "M", "M")
#Code the data according to which drug is associated with the score
drug = c(rep("A",9), rep("B",9), rep("C",9))
#Create data frame with pain scores, coded by which drug the patient took
migraine = data.frame(pain,drug)
#Look at our data frame
migraine
## pain drug
## 1 4 A
## 2 5 A
## 3 4 A
## 4 3 A
## 5 2 A
## 6 4 A
## 7 3 A
## 8 4 A
## 9 4 A
## 10 6 B
## 11 8 B
## 12 4 B
## 13 5 B
## 14 4 B
## 15 6 B
## 16 5 B
## 17 8 B
## 18 6 B
## 19 6 C
## 20 7 C
## 21 6 C
## 22 6 C
## 23 7 C
## 24 5 C
## 25 6 C
## 26 5 C
## 27 5 C
#Run a one-way ANOVA
results = aov(pain ~ drug, data=migraine)
summary(results)
## Df Sum Sq Mean Sq F value Pr(>F)
## drug 2 28.22 14.111 11.91 0.000256 ***
## Residuals 24 28.44 1.185
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#Post hoc analysis using Tukey's HSD
TukeyHSD(results, conf.level = 0.95)
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = pain ~ drug, data = migraine)
##
## $drug
## diff lwr upr p adj
## B-A 2.1111111 0.8295028 3.392719 0.0011107
## C-A 2.2222222 0.9406139 3.503831 0.0006453
## C-B 0.1111111 -1.1704972 1.392719 0.9745173
#Add column full of gender info to migraine dataset
migraine$gender <- c("F", "F", "F", "M", "M", "M", "M", "F", "F", "M", "M", "F", "F", "F", "M", "F", "M", "M", "M", "F", "F", "F", "F", "M", "F", "M", "M")
migraine
## pain drug gender
## 1 4 A F
## 2 5 A F
## 3 4 A F
## 4 3 A M
## 5 2 A M
## 6 4 A M
## 7 3 A M
## 8 4 A F
## 9 4 A F
## 10 6 B M
## 11 8 B M
## 12 4 B F
## 13 5 B F
## 14 4 B F
## 15 6 B M
## 16 5 B F
## 17 8 B M
## 18 6 B M
## 19 6 C M
## 20 7 C F
## 21 6 C F
## 22 6 C F
## 23 7 C F
## 24 5 C M
## 25 6 C F
## 26 5 C M
## 27 5 C M
#Run two-way ANOVA using gender and drug as factors
results = aov(pain ~ drug*gender, data=migraine)
summary(results)
## Df Sum Sq Mean Sq F value Pr(>F)
## drug 2 28.222 14.111 28.088 1.16e-06 ***
## gender 1 0.002 0.002 0.004 0.952
## drug:gender 2 17.893 8.946 17.808 3.00e-05 ***
## Residuals 21 10.550 0.502
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#Post hoc analysis on two-way ANOVA
TukeyHSD(results, conf.level = 0.95)
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = pain ~ drug * gender, data = migraine)
##
## $drug
## diff lwr upr p adj
## B-A 2.1111111 1.268923 2.9532993 0.0000084
## C-A 2.2222222 1.380034 3.0644104 0.0000040
## C-B 0.1111111 -0.731077 0.9532993 0.9410333
##
## $gender
## diff lwr upr p adj
## M-F -0.01648352 -0.5842182 0.5512512 0.9524246
##
## $`drug:gender`
## diff lwr upr p adj
## B:F-A:F 0.30 -1.1875023 1.78750227 0.9873049
## C:F-A:F 2.20 0.7975694 3.60243059 0.0009237
## A:M-A:F -1.20 -2.6875023 0.28750227 0.1619424
## B:M-A:F 2.60 1.1975694 4.00243059 0.0001207
## C:M-A:F 1.05 -0.4375023 2.53750227 0.2752703
## C:F-B:F 1.90 0.4124977 3.38750227 0.0074874
## A:M-B:F -1.50 -3.0679651 0.06796506 0.0660199
## B:M-B:F 2.30 0.8124977 3.78750227 0.0010862
## C:M-B:F 0.75 -0.8179651 2.31796506 0.6700989
## A:M-C:F -3.40 -4.8875023 -1.91249773 0.0000064
## B:M-C:F 0.40 -1.0024306 1.80243059 0.9441652
## C:M-C:F -1.15 -2.6375023 0.33750227 0.1947322
## B:M-A:M 3.80 2.3124977 5.28750227 0.0000011
## C:M-A:M 2.25 0.6820349 3.81796506 0.0024216
## C:M-B:M -1.55 -3.0375023 -0.06249773 0.0379545
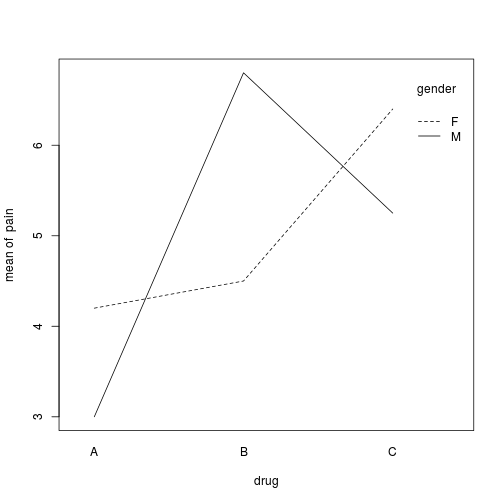
#Plot the interaction for our two-way ANOVA
interaction.plot(drug, gender, pain)
#Create bachelor dataset for correlation demo
weeks = c(8,7,6,5,4,4,3,3,3,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1)
age = c(24,23,25,24,23,22,27,28,23,30,27,30,24,27,29,30,27,29,25,34,27,22,25,28,28,23)
bachelor = data.frame(weeks, age)
bachelor
## weeks age
## 1 8 24
## 2 7 23
## 3 6 25
## 4 5 24
## 5 4 23
## 6 4 22
## 7 3 27
## 8 3 28
## 9 3 23
## 10 2 30
## 11 2 27
## 12 2 30
## 13 1 24
## 14 1 27
## 15 1 29
## 16 1 30
## 17 1 27
## 18 1 29
## 19 1 25
## 20 1 34
## 21 1 27
## 22 1 22
## 23 1 25
## 24 1 28
## 25 1 28
## 26 1 23
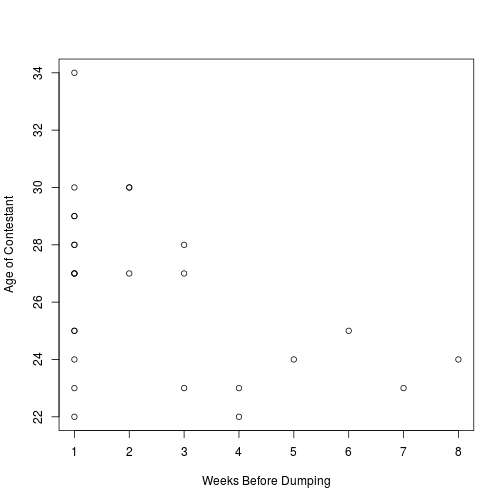
#Run test of correlation on bachelor data - default method is Pearson correlation
cor.test(bachelor$weeks, bachelor$age)
##
## Pearson's product-moment correlation
##
## data: bachelor$weeks and bachelor$age
## t = -2.3978, df = 24, p-value = 0.02463
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.70663528 -0.06298623
## sample estimates:
## cor
## -0.4396126
plot(bachelor$weeks, bachelor$age, xlab="Weeks Before Dumping", ylab="Age of Contestant")
#Supplemental: Another kind of post hoc test (pairwise t-tests with a bonferroni correction) on the migraine dataset
pairwise.t.test(pain, drug, p.adjust="bonferroni")
##
## Pairwise comparisons using t tests with pooled SD
##
## data: pain and drug
##
## A B
## B 0.00119 -
## C 0.00068 1.00000
##
## P value adjustment method: bonferroni
#Supplemental: Another way to do a t-test on the migraine dataset
with(migraine, t.test(pain[drug == "A"], pain[drug == "B"]))
##
## Welch Two Sample t-test
##
## data: pain[drug == "A"] and pain[drug == "B"]
## t = -3.6909, df = 12.896, p-value = 0.002751
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -3.3478073 -0.8744149
## sample estimates:
## mean of x mean of y
## 3.666667 5.777778
Python-ized version (courtesy of @QuLogic)

